[백준]BOJ #1450: 냅색문제

문제 출처: https://www.acmicpc.net/problem/1450

문제

세준이는 N개의 물건을 가지고 있고, 최대 C만큼의 무게를 넣을 수 있는 가방을 하나 가지고 있다.

N개의 물건을 가방에 넣는 방법의 수를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N과 C가 주어진다. N은 30보다 작거나 같은 자연수이고, C는 10^9보다 작거나 같은 음이아닌 정수이고. 둘째 줄에 물건의 무게가 주어진다. 무게도 10^9보다 작거나 같은 자연수이다.

출력

첫째 줄에 가방에 넣는 방법의 수를 출력한다.

예제 입력 1

2 1
1 1

예제 출력 1

문제 분석
1. Brute Force 로 모든 경우의 수를 구한다고 생각할 경우 2^30 번의 연산을 해야 함. 대략 10억이므로 10초로 어림잡아도 시간초과
2. 2^15==32768 이므로 Meet in the middle로 연산횟수 줄일 수 있다.
3. N개의 input 무게 배열을 절반으로 나누어 양쪽 부분에서 가능한 모든 경우의 수를 연산한 후 vector에 저장
4. 다른 한 쪽을 정렬한 뒤 정렬하지 않은 쪽 vector를 순회하며 조합 가능한 가짓수를 더함

문제 풀이( 코드)

#include <bits/stdc++.h>
#define MAX 31
#define INF 1e9
#define pii pair<int, int> 
#define foi(n) for(int i=0;i<n;++i)
#define foj(n) for(int j=0;j<n;++j)
#define endl '\n'
#define ll long long
#define vi vector<int> 
  
using namespace std;
  
int N, C, weight[31];
vector<ll> l_part, r_part;
  
void init(){
    cin>>N>>C;
    foi(N) cin>>weight[i];
}
void leftCase(int idx, int sum){
    if(sum>C) return;
    if(idx==N/2){
        l_part.push_back(sum);
        return;
    }
    leftCase(idx+1, sum);
    leftCase(idx+1, sum+weight[idx]);
}
void rightCase(int idx, int sum){
    if(sum>C) return;
    if(idx==N){
        r_part.push_back(sum);
        return;
    }
    rightCase(idx+1, sum);
    rightCase(idx+1, sum+weight[idx]);    
}
void solve(){
    int mid=N/2;
    // Compute subsets of right and left partitions
    leftCase(0, 0);
    rightCase(N/2, 0);
    // Sort right partition for binary search
    sort(r_part.begin(), r_part.end());	
    ll cnt=0;
    // Traverse all elments of left partition and do Binary Search
    // for a pair in right partition with sum less than C
    for(int i=0;i<l_part.size();i++){	
        cnt+=upper_bound(r_part.begin(), r_part.end(), C-l_part[i])-r_part.begin();
    }
    cout<<cnt;
}
  
int main(){
    init();
    solve();
}

Point
1. Meet in the middle 은 input의 크기가 작지만 brute force를 사용할 수 있을 정도로 작진 않은 경우에 사용되는 탐색 알고리즘이다. 분할 정복과 같이 문제를 두 개로 나누어 각각을 연산한 뒤 다시 merge한다. 하지만 나뉜 문제가 기존 문제와 동일한 구조를 가지지 않기 때문에 분할 정복과 같이 Meet in the middle을 적용할 수는 없다.
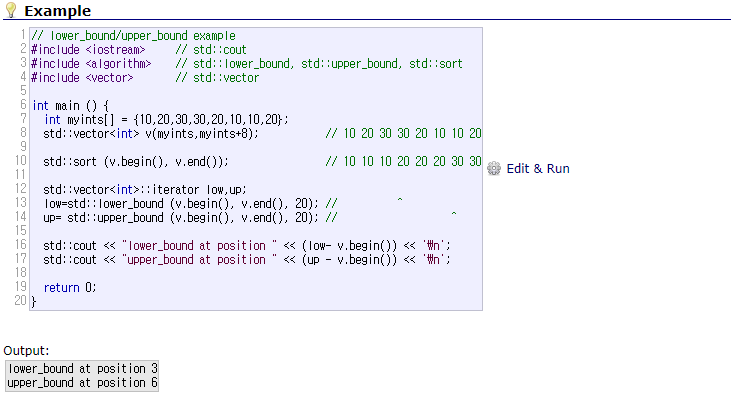
2. lower_bound는 value 값과 동일한 값이 있을 때, 그 값의 가장 첫번째 위치를 반환함. upper_bound는 같은 경우에 그 값의 마지막 위치+1 을 반환.

Reference

문제

입력

출력

예제 입력 1

예제 출력 1

문제 분석

문제 풀이( 코드)

Point

Reference